试析基坑开挖与支护模拟的位移迭代法

　　试析基坑开挖与支护模拟的位移迭代法

　　林鹏文

　　(安溪县住房和城乡规划建设局，省 市 362400)

　　摘要：鉴于目前基坑工程的发展和一些现状，本文分析了对基坑开挖后坑体周围土体的一些变化，为了更好的模拟基坑工程中支护结构的受力和变形情况，用位移迭代法，通过工程实例进行了验证，模拟与结果基本吻合，证明了此法可行，从而有效的解决了基坑数值模拟中存在的一些问题，最后用位移迭代法探究了个各种因素对基坑支付的守和变形的影响，以期为插入支护桩的深度、土体加固的深度等等参数的选择提供一些参考。

　　关键词：基坑 支护模拟 位移迭代法 有限元法

　　随着地下空间的大量开发和利用以及高层建筑的增加，使得许多的的基坑工程涌现出来。在国外有许多比较著名的地下工程，比如巴黎的中央商场、日本东京的八重洲地下街等等。我过近些年来也出现了很多的地下工程，当前最深的基坑工程深度已经达到了32m。但是在目前我国的基坑工程中国，还存在着许多的问题，事故频发，所以，无论是从时间上还是理论上，对基坑工程的研究都是十分具有现实意义的。

　　1我国基坑工程的研究方法

　　随着高层建筑和底下工程的不管出现，基坑工程也开始受到人们越来越多的重视，于是基坑的开挖和支护问题就不可避免的也随之出现了。在基坑工程的研究中，主要涉及到三个方面的问题，即：支护结构、基坑的稳定性问题以及土体的变形问题。研究基坑工程的方法也有很多种，比如模型观测、工程经验等。在进行基坑理论计算的时候时候，最长用的方式是极限平衡法、土抗力法以及位移迭代法。其中位移迭代法可以从时间和空间上全面的反映各种元素对支护结构以及基坑周围土体的受力和位移的情况，所以在应用上的前景比较广阔。位移迭代法中利用有限元模型进行数值分析在基坑中又是最常用的一种方法，它主要包括弹性地基杆有限元法和连续介质有限元法两种：

　　1）弹性地基杆有限元法：这是一种比较简单的方法，因此在基坑工程中经常可以看到。主要是因为此种方法是建立在线弹性本构关系上，不用考虑土体的弹塑性以及土压力随位移的变化情况，所以在实际中，这种方法有它的明显的缺点，就是不能真实的反映土以及结构在位移和荷载上的变化情况。

　　2）连续价值有限元法：这种方法在桩土间采用的是接触面单元，考虑桩土的共同作用。在岩土工程中常常用到的接触面单元是Goodman 接触面单元[1]和Desai薄层接触面单元[2]。Goodman接触面单元的概念比较清楚，只要给出接触面法向刚度Kn与切向刚度 Ks，那么，从应用工程的角度来看，这种方法是很方便且易行的，不过在法向刚度的取值上，它要求的数值比较大，目的是为了防止嵌入的过量，但是也就导致了这种人为设置的法向刚度使得法向应力的误差增大。Desai薄层接触面单元引入了嵌入控制的方法，所以在很大程度上克服了上述单元的缺点，而且在接触面的参数上，是三个独立的参数即：剪切模量G、弹性模量 E、和泊松比u。

　　2位移迭代法的有限元模型

　　（一）2.1建立模型

　　下面通过具体实例进行位移迭代法的优先模型分析，如下图1所示：.

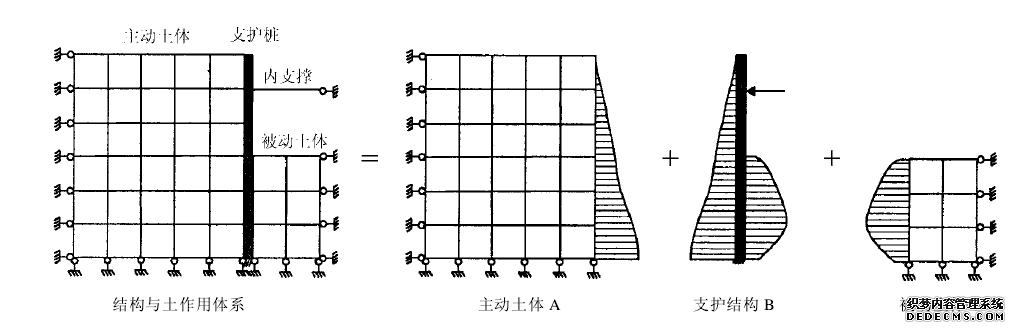
　　图1 名称

　　1、我们取一断面通过平面问题分析，根据对称性，截取模型的1/2，将整体模型分成上图中的三部分：即主动土体A、支护结构B以及被动土体C，其中：

　　A部分：所承受的荷载为重力，左侧的边界条件是水受平方向固定约束，右侧的边界条件是支护桩的反力，而底部的边界条件受垂直方向固定约束的，模拟的方式是通过四边形单元来进行模拟，节点可以是4，5，8，9等节点，土体通常使用的是弹塑性本构模型。

　　B部分：在不考虑自重的前提下，边界条件是两侧的压力，其中右侧开挖的部分是自由边界，底部是固定约束。

　　C部分：所承受的荷载一样也是重力，左侧的边界条件是支护桩的反力，右侧的边界条件是水平方向的固定约束，正好与A部分是相反的，底部同样是垂直方向的固定约束。通常也是采用的四边形面单元。

　　（二）2.2模型计算

　　用位移迭代法将模型中的三个独立部分分别进行计算，在三个模型中输入桩体界面上的相互作用力或者位移作为边界的条件，我们可以假设支护桩的侧壁光滑，并且以桩体不变形作为初始条件，那么通过反复的迭代就可以使桩土接触处的位移和水平应力相等，从而作为求解稳定的条件。如果是面对多次开挖的基坑，可以将初始条件设置为上一次开挖变形稳定后的位移，然后用同样的方法进行迭代。

　　（三）2.3位移迭代法的实现流程

　　1、）分别对模型A、B、C建立有限元方程：

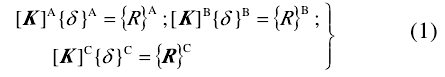
　　公式中：[K]——总刚度矩阵；{}——节点位移列阵；{R}——荷载列阵；上表表示不同的模型。

　　2）将模型的三个有限元方程按照位移向量重组，使得桩土共节点处的水平位移集中到一起，并将坑底以上和以下的位移分开，并对刚度矩阵和荷载列阵分块，即得到以下公式：

　　公式中：{AB}、{AC}分别基坑底面以上和以下支护桩的位移；{R1AB}、{R2AB}分别是基坑底面以上和以下的A对B的作用力；{R2CB}是基坑底面以下C对B的作用力；{A}、{C}是除{AB}、{AC}以外的节点位移分量的列阵；{R3A}、{R3C}是{A}、{C}对应的节点荷载，[KijA,B,C]是各个模型总刚度矩阵的子块。

　　3）前面说了，如果在只进行一次开挖的情况下，计算的时候讲初始条件设置为支护桩桩体不变形，即{AB}0={0}，{AC}0={0}，通过方程式（2）（4），可以求得约束结点的水平结点力{R1AB}0、{R2AB}0、{R2CB}0。

　　4）将{R1AB}0、{R2AB}0、{R2CB}0作为边界条件再代入（2）（3）（4）中，进而可以求得支护桩个结点的位移{AB}1、{AC}1。

　　5）将上述{AB}1、{AC}1代入（2）（4）公式中，分别求得约束结点的水平结点力{R1AB}1、{R2AB}1、{R2CB}1。

　　6）再将{R1AB}1、{R2AB}1、{R2CB}1代入公式（3）中，求得支护桩各结点的位移{AB}2、{AC}2。

　　7）对两次求解的结果进行比较，当其中对应的元素结果值相等时就可以终止计算，从而获得支护桩与土体的相关参数。在实际中，可以使用相对误差来判定。

　　8）当误差相差太大，不在允许的范围内时，那么就要继续重复2——6的步骤，直到结果满足为止，迭代结束。

　　9）对于多次开挖的基坑工程，初始条件设置为上一次位移计算的结果，即{AB}0={u10}、{AC}0={u20}，然后重复2——6的步骤。

　　3结束语

　　综上所述，在基坑开挖和支护模拟的研究中，其他的研究方法要么就是没有考虑支护结构的变形，要么就是接触面单元的弹性参数不容易确定，所以有着自身明显的弊端，而位移迭代法从根本上弥补了这些方法上的不足，通过建立三个相对独立的模型，各自进行计算，当进行两次或者几次移迭代计算，得出的结果相等时，迭代完成，此时得出的力和位移就可以作为基坑支护结构稳定后的受力和变形，因而位移迭代法比较全面客观的反映了结构与土体相互作用的动态过程，因此，在以后的基坑开挖和支护模拟的研究中应用的前景非常广阔。

　　参考文献：

　　[1]李萍,邓小鹏,相建华,李同录. 基坑开挖与支护模拟的位移迭代法[J]. 岩土力学,2005,11:124-127.

　　[2]邓小鹏. 深基坑开挖与支护有限元数值分析[D].长安大学,2004.

　　[3]张云. 深基坑工程开挖与支护的ANSYS有限元模拟[D].中国海洋大学,2008.

　　[4]聂淼. 深基坑开挖过程数值模拟及支护对策[D].贵州大学,2009.

　　[5]张峰. 深基坑板桩支护模型试验研究[D].武汉科技大学,2007.

　　[6]杨新忠. 基于有限单元法的深基坑支护体系变形研究[D].河海大学,2007.